1.3 – Flow Rate

1.3.0 – Learning Objectives

By the end of this section you should be able to:

  1. Understand the concept of flow rate.
  2. Convert one type of flow rate into another.
  3. Know how flow rates are measured.
  4. Have a basic understanding of differential pressure.

1.3.1 – Introduction

Almost every process involves the movement of material from one point to another. The movement of material is present between process units, production facilities, and transportation depots. The rate at which materials are transported is the flow rate.

1.3.2 – Mass Flow Rate

Mass flow rate is the measurement of mass per unit time (mass/time). This flowrate is usually denoted by the character \(\dot{m}\), where \(\dot{m} = \frac{ kg }{s}\). Since mass must be conserved, the input masses of a process must equal the output masses, unless there is accumulation (See section 1.8.2 for further reference). Therefore, mass flowrate is a very useful tool in solving material balances.

1.3.3 – Molar Flow Rate

Molar flow rate is the measurement of moles per unit time (mole/time). This flowrate is usually denoted by the character $ :raw-latex:`\dot{n}` $, where $ :raw-latex:`\dot{n}` = :raw-latex:`\frac{ moles }{s}` $. Since the total number of moles of atomic species (eg. N, O, C) must be conserved, it is useful in solving both reactive and non-reactive problems.

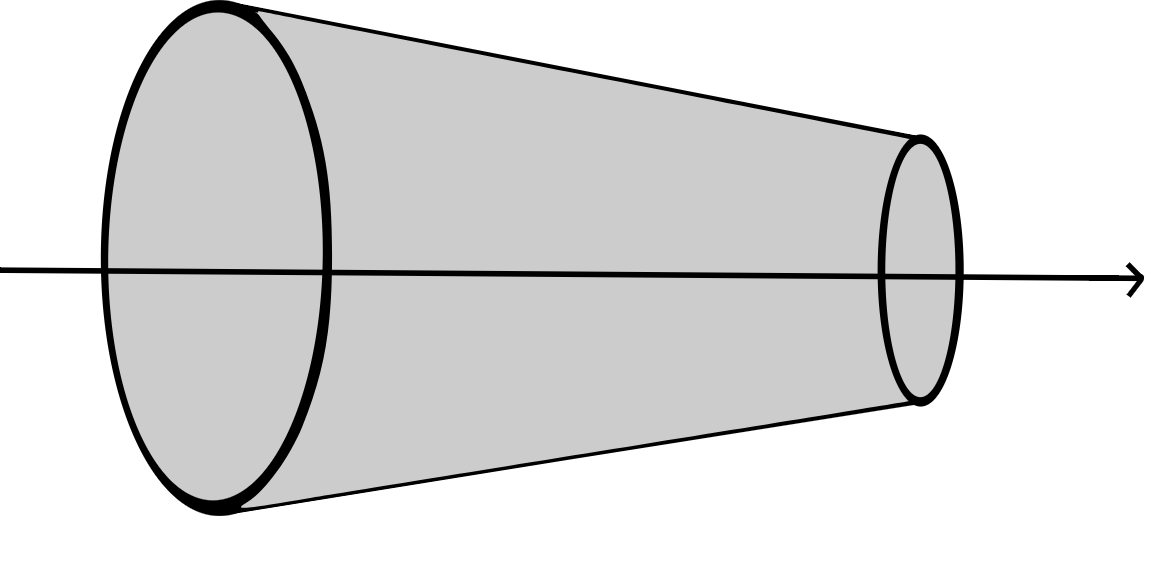
1.3.4 – Volumetric Flow Rate

Volumetric flow rate is the measurement of volume per unit time (volume/time) This flow rate is usually denoted by the character \(\dot{V}\), where \(\dot{V} = \frac{ m^3 }{s}\). Volumetric flow rate may change with density.

\[\rho = \frac{m}{V} = \frac{\dot{m}}{\dot{V}} = \frac{\frac{kg}{s}}{\frac{m^3}{s}} = \frac{kg}{m^3}\]
\[\dot{m} = \rho \dot{V}\]

Since mass flow rate is more useful, but volumetric flow rate is easier to measure, we use the formula shown above to convert from one basis to another.

Although density is nearly conserved for solids and liquids, it is not for gases. For example, if a gas is flowing through a nozzle, the mass flow rate will not change but the gas will compress or expand.

Attribution: Said Zaid-Alkailani & UBC [CC BY 4.0 de (https://creativecommons.org/licenses/by/4.0/)]

1.3.5 – Flow Rate Measurement

Flow rates are measured by a device called a flowmeter. This device provides a continuous reading of the flow rate in the line. Two commonly used flowmeters are rotameters and orifice meters.

1. Rotameters

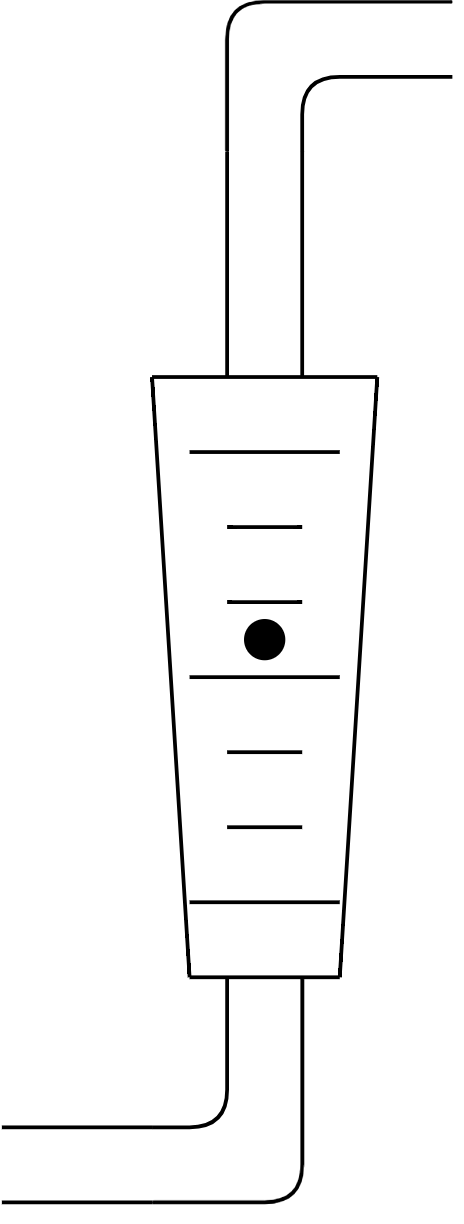
Attribution: Said Zaid-Alkailani & UBC [CC BY 4.0 de (https://creativecommons.org/licenses/by/4.0/)]

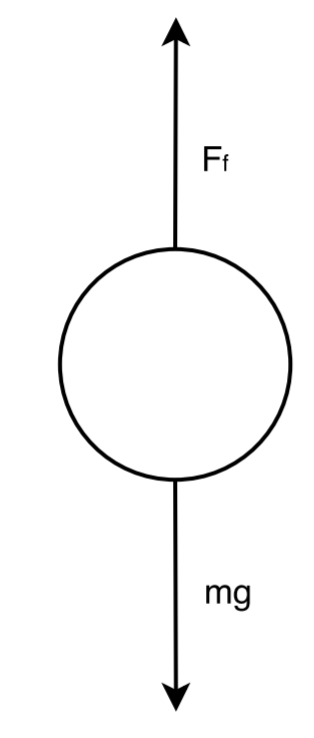
Rotameters are a tapered vertical tube containing a small ball (the black dot in the image). The larger the flow rate, the higher the ball rises due to the increased friction force.

2. Orifice Meters

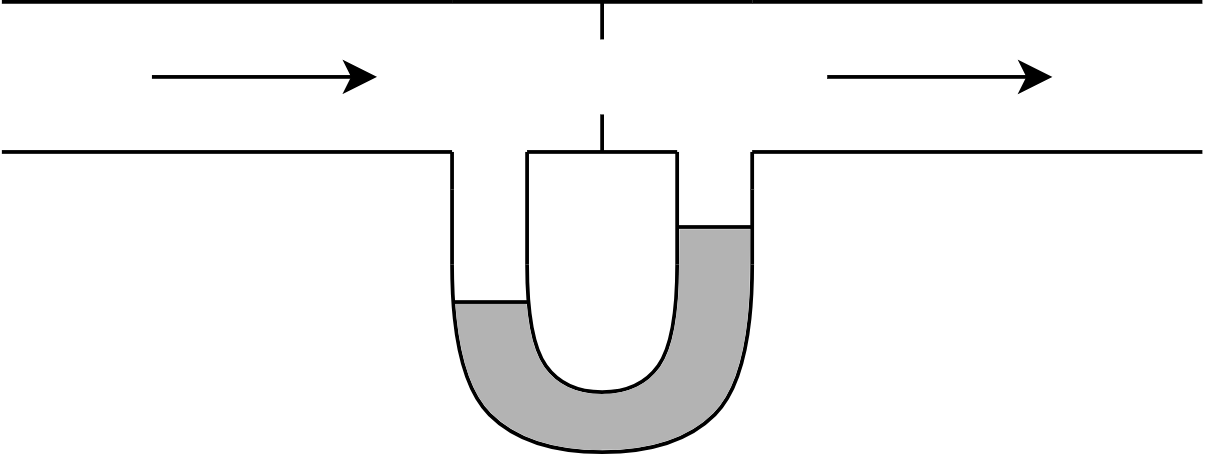
Attribution: Said Zaid-Alkailani & UBC [CC BY 4.0 de (https://creativecommons.org/licenses/by/4.0/)]

The orifice meter is an obstruction in the flow channel which causes a pressure drop. The magnitude of the pressure drop dictates the flow rate. The larger the pressure drop, the larger the flow rate. A manometer measures the pressure drop.

1.3.6 – Manometer

Manometers are one of the earliest tools used in measuring pressure drops. This is done by measuring the heights of the different fluids in the manometer.

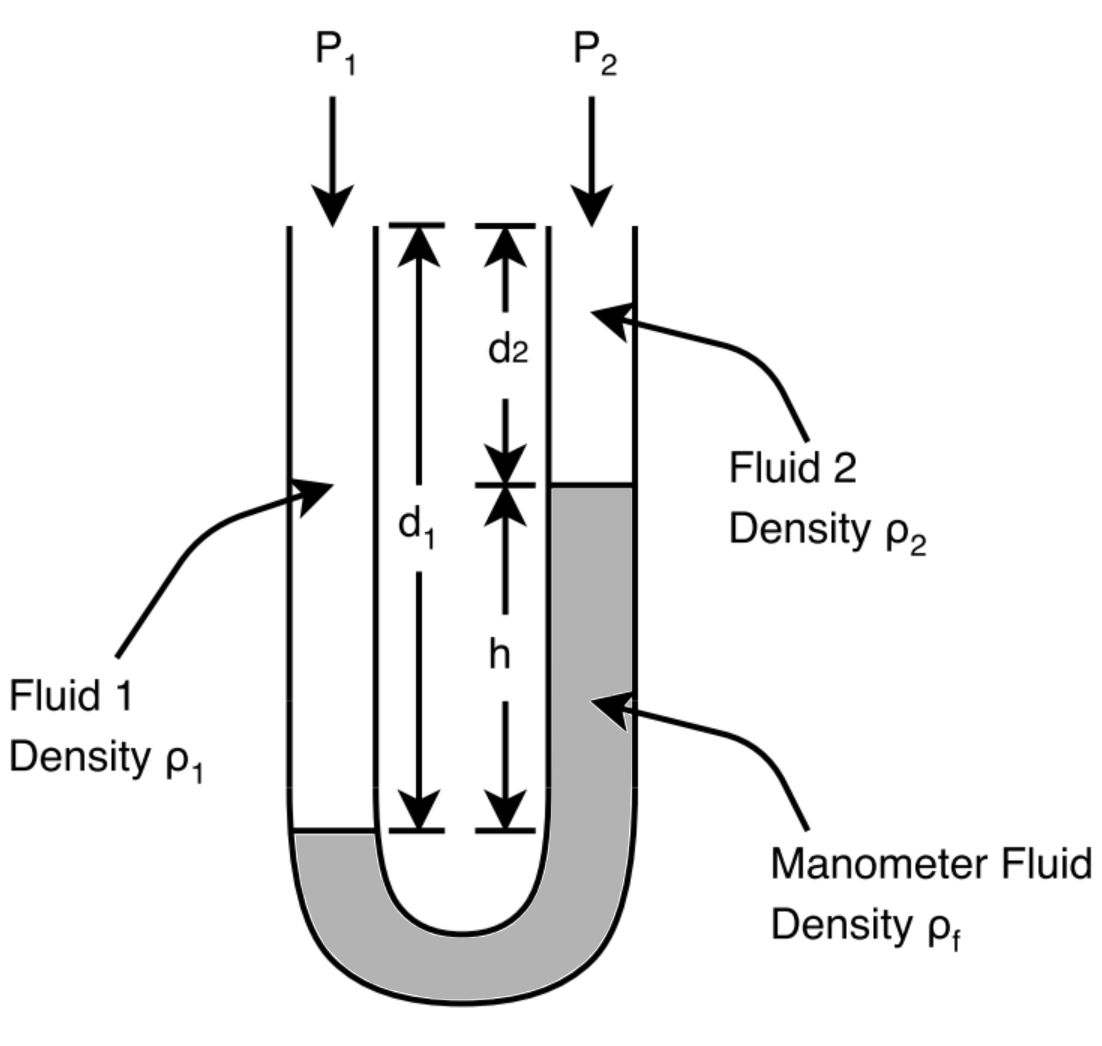
Attribution: Said Zaid-Alkailani & UBC [CC BY 4.0 de (https://creativecommons.org/licenses/by/4.0/)]

Writing and equation the expressions for the pressures at points (a) and (b) in the figure shown above, we get the general manometer equation:

\[P_1 + \rho_1 g d_1 = P_2 + \rho_2 g d_2 + \rho_f g h \quad \text{(General Manometer Equation)}\]

If the densities of fluids 1 and 2 are the same, the equation simplifies to:

\[P_1 - P_2 = (\rho_f - \rho) g h \quad \text{(Differential Manometer Equation)}\]

If fluids 1 and 2 are gases, the equation simplifies further to:

\[P_1 - P_2 = \rho_f g h \quad \text{(Manometer Formula for Gases)}\]

1.3.7 – Problem Statement

Question

A differential manometer is used to measure the drop-in pressure between two points in a process line containing water. The density of the manometer fluid is \(1.10 \space g/cm^3\). The density of the fluid that is flowing is \(1.00 \space g/cm^3\). The measured levels in each arm are shown below. Calculate the pressure drop in pascals.

Attribution: Said Zaid-Alkailani & UBC [CC BY 4.0 de (https://creativecommons.org/licenses/by/4.0/)]

Answer

In [1]:

#Declare all known varibles

rho = 1000  # kg/m^3
rho_f = 1100 # kg/m^3
g = 9.81 # m/s^2
h = 0.392 - 0.334 # m

#Solve for pressure drop using Differential Manometer Equation

P_drop = (rho_f-rho)*g*h

#Print Results

print("The pressure drop is measured to be ", P_drop, "Pa")

The pressure drop is measured to be  56.897999999999996 Pa

As you can see the value we get is not exactly 56.898 Pa due to rounding error by the computer, but if you take significant figures into account the final answer is \(P_1 - P_2 = 56.9 \space Pa\).

In [ ]: